Crash The Casino Game - Valentina

Valentina was a project created to explore the mathematics behind the game crash. Crash is a game casinos and gambling sites have.

Who is Valentina Tereshkova?

Valentina Tereshkova was the first woman to travel into space. Flying her solo mission in 1963 at just 26-years-old, that makes her one of the youngest women to embark on a solo mission to this day.

She orbited Earth 48 times and completed her mission after 3 or so days in space.

As a child, Valentina always wanted to pursue a career in science. She was able to achieve such a dream by becoming a cosmonaut and later being appointed the leader of the Committee for Soviet Women by the Soviet space program, and a Soviet representative speaking on women in science at the World Peace Council (1966).

Her influence has given many women a light to look up to when pursuing a field in STEM.

Valentina Tereshkova | Biography

Valentina Tereshkova, Soviet cosmonaut, the first woman to travel into space.

What is this project about?

Valentina was a project created to explore the mathematics behind the game crash. Crash is a game casinos and gambling sites have. The game is straightforward, players bet an amount at the start of the game, then a multiplier value (ie. 2.00x, 3.33x) increases from 1.00x and crashes at some random value. Players can cash out and make their initial value times their cashed-out multiplier. If the value crashes before they cash out, the player loses the amount they bet.

I'm not a fan of gambling, but I am a fan of statistics and wondered why companies allow this game.

The Math Behind Crash

Casinos use the equation as found on Roobet's Fairness page, many post their source code which is part of their 'fairness' policy. And most of them use the same equation.

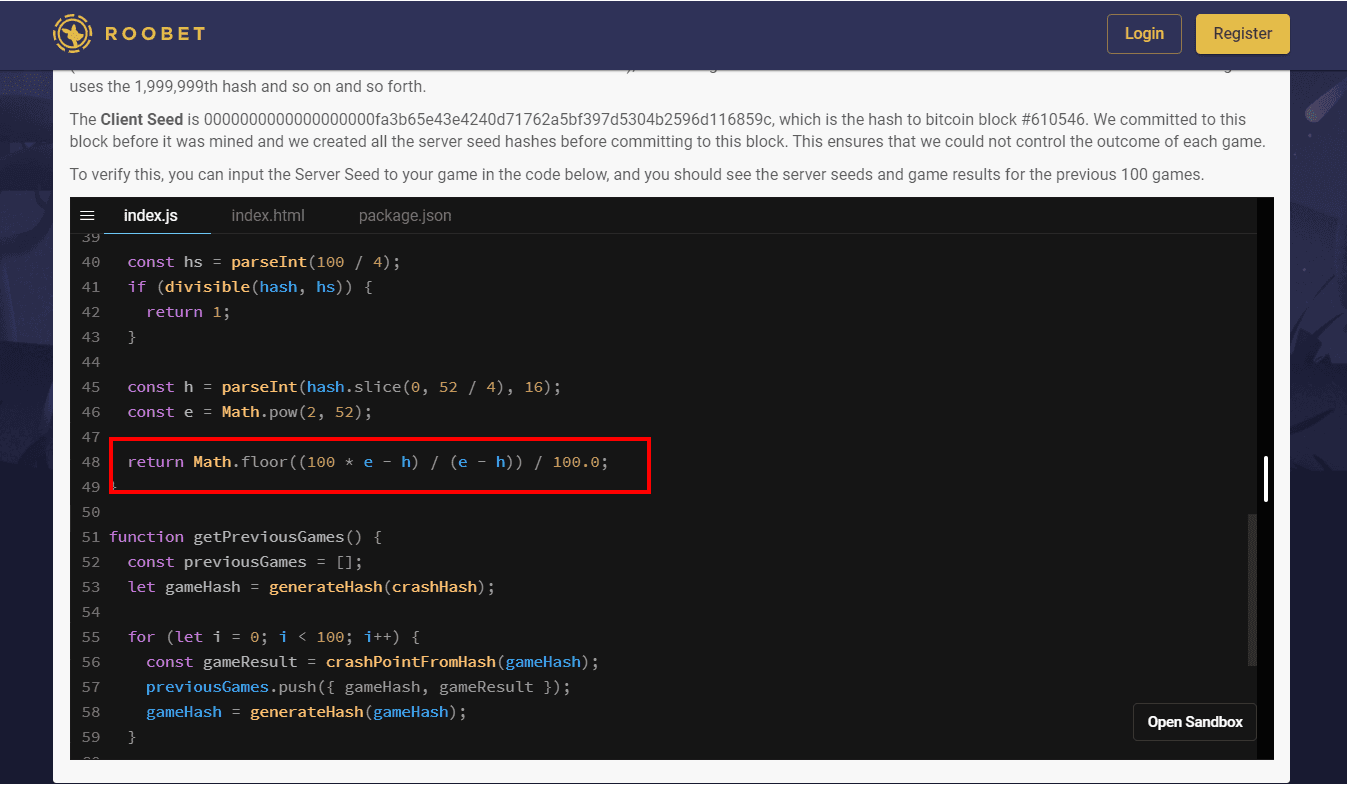
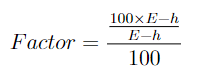
E is some extreme value and is the location of the vertical asymptote (limit). Lots of Casinos use 2⁵² Which is also what we are going to do since this is usually the limit number of bits allowed for Double-precision binary floating-point (the double datatype). IEEE 754 specifies double storing Significand precision at 52 bit explicitly stored.

Note: Here is the equation on Stake.com though they use 2³² as their E value

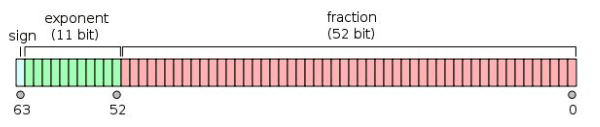
h is a number chosen uniformly at random between 0 and E-1 (inclusively)

Using these factors

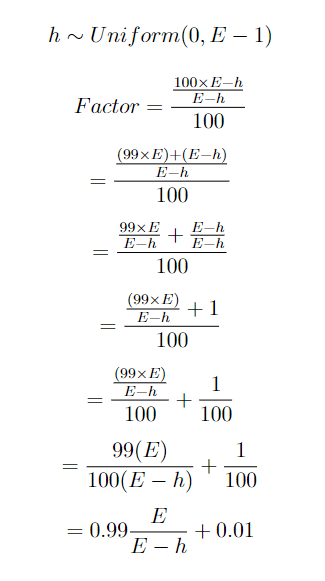
The Equation simplifies to 0.99(E/E-h) + 0.01

I've added a growth rate to the equation (as expressed below), this isn't something that casinos do, but it is something that can be done to heavily skew the results towards one side.

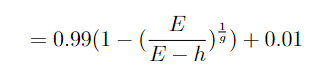
where g ≠ 0

Using this equation we can get calculate an estimated CDF and EV value, I used the help of my library friend Numpy :)

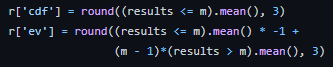
For the EV we are assuming a 1-dollar bet and exiting the bet each time the multiplier reaches a value of m. Where m is some arbitrary multiplier. This was calculated with a sample size of 100k, so it isn't perfectly accurate but a good approximation.

With a growth rate of 1, we get an expected value curve of the following

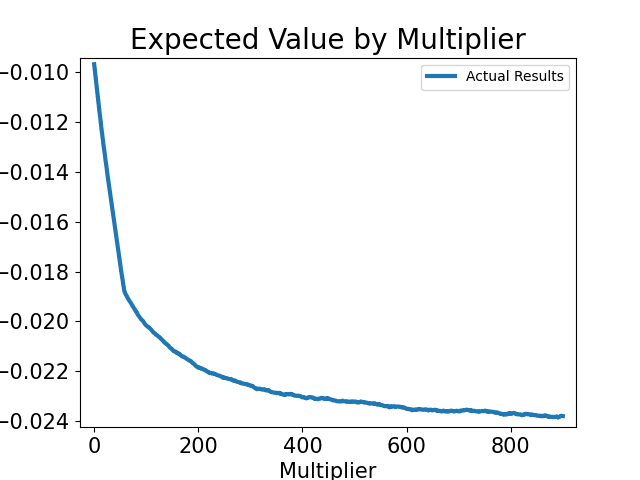
The Y-axis is the expected return, and the X-axis is the multiplier cashed out. (Note: 200 = 2.00x, 400 = 4.00x, 600 = 6.00x)

Regardless of the cashed-out choice, the EV always results in a loss (a return below 0).

Though, it is possible to have an expected win if the growth value is greater than 0 and less than 1. However, this growth value is controlled by the casino, and I don't think any company is dumb enough to do something that puts them out of business.

You can test out different values using the calculator on Valentina.

And I've posted the source code on my GitHub repo for anyone curious.

Valentina | Github Repository

Crash - Casino/Gambling Game - Simulates the game Crash and can calculate the expected value of winning/losing the game.

Project Link

Here you can simulate the game or calculate the possible returns

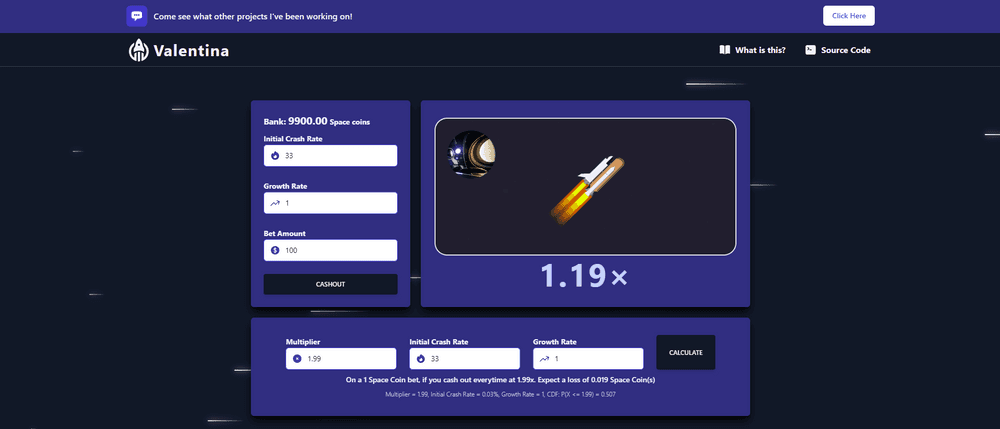
Valentina | Crash Casino Game

Crash - Casino/Gambling Game - Simulates the game Crash and can calculate the expected value of winning/losing the game.

What I haven't figured out.

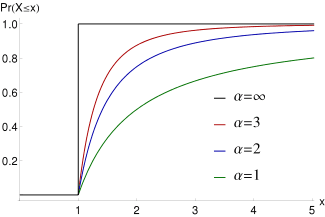
I still haven't found the expected CDF or the EV Equations, I can only estimate and graph it through high sample sizes, I suspect the curve follows Pareto Distribution, with its CDF denoted as something along the lines of 1-(x_m/x)^g

Where x_m represents the scale parameter and g is the shape or growth rate. The image below shows different growth rates. In this case, our growth rate will be the inverse of g since our distribution is reflected horizontally compared to a regular Pareto Distribution.

What is the meaning behind the project name?

I've written a post about the meaning behind my project names, you can read about it here.

Built with Next.js and Tailwind CSS. Made with ❤️ by Justin Zhang.